|
I've spent the last two weeks trying to solve what is on the surface a relatively straightforward problem in 3D geometry. Maybe writing a little discourse on it will help me get things straight. Or maybe someone will read this and tell me this problem has been solved ages ago. Either way, let's go.
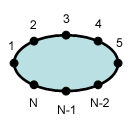 Say you've got a set of 2D vertices defining a region. The vertices are numbered 1 through N, giving the order in which you connect them to draw the region's outline. So far, no problem. Say you've got a set of 2D vertices defining a region. The vertices are numbered 1 through N, giving the order in which you connect them to draw the region's outline. So far, no problem.
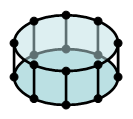 Now let's extend our region in the third dimension, giving it thickness. So now we've got TWO sets of identical vertices, offset along the vertical axis by the thickness of the region. All's still good. Now let's extend our region in the third dimension, giving it thickness. So now we've got TWO sets of identical vertices, offset along the vertical axis by the thickness of the region. All's still good.
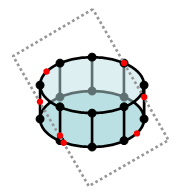 Here's where things begin to get interesting. Now let's say you wanted to slice this 3D region with some plane and draw the cross section. Since the plane may slice between vertices, you have to look for intersections of the links joining the vertices, both the links within the upper and lower regions and the links between them, with the plane. This still is a relatively easy thing to do. So when you finish this, you've now got a set of M intersection points lying within the plane. Now you want to connect these points and draw your cross section. But in what order do you connect them? At first glance it seems relatively simple, but i can't seem to find a straightforward solution, either analytic or algorithmic, to this question. You have three types of intersections: intersections between the upper vertices, intersections between the upper and lower vertices, and intersections between the lower vertices. There should be some way to figure out, based on the connectivity of the original regions, the order in which the intersections are laid out. Here's where things begin to get interesting. Now let's say you wanted to slice this 3D region with some plane and draw the cross section. Since the plane may slice between vertices, you have to look for intersections of the links joining the vertices, both the links within the upper and lower regions and the links between them, with the plane. This still is a relatively easy thing to do. So when you finish this, you've now got a set of M intersection points lying within the plane. Now you want to connect these points and draw your cross section. But in what order do you connect them? At first glance it seems relatively simple, but i can't seem to find a straightforward solution, either analytic or algorithmic, to this question. You have three types of intersections: intersections between the upper vertices, intersections between the upper and lower vertices, and intersections between the lower vertices. There should be some way to figure out, based on the connectivity of the original regions, the order in which the intersections are laid out.
This little sample case is just the tip of the iceberg though. What if your plane cuts a single region into two separate cross sections? For example, slicing a donut? You now have to figure out how to connect the intersections, and how to separate them into individual regions!
My common sense is telling me this is a problem that the graphics community must have solved long ago, but i can't find anything about it online. It's a subtly different question than your typical ray-tracing engine deals with, so it may not have been figured out. Or it has, but it's a proprietary algorithm that isn't freely distributed. At any rate, somebody help me! This is driving me nuts!
|  previous
previous
 previous
previous
 Say you've got a set of 2D vertices defining a region. The vertices are numbered 1 through N, giving the order in which you connect them to draw the region's outline. So far, no problem.
Say you've got a set of 2D vertices defining a region. The vertices are numbered 1 through N, giving the order in which you connect them to draw the region's outline. So far, no problem. Now let's extend our region in the third dimension, giving it thickness. So now we've got TWO sets of identical vertices, offset along the vertical axis by the thickness of the region. All's still good.
Now let's extend our region in the third dimension, giving it thickness. So now we've got TWO sets of identical vertices, offset along the vertical axis by the thickness of the region. All's still good. Here's where things begin to get interesting. Now let's say you wanted to slice this 3D region with some plane and draw the cross section. Since the plane may slice between vertices, you have to look for intersections of the links joining the vertices, both the links within the upper and lower regions and the links between them, with the plane. This still is a relatively easy thing to do. So when you finish this, you've now got a set of M intersection points lying within the plane. Now you want to connect these points and draw your cross section. But in what order do you connect them? At first glance it seems relatively simple, but i can't seem to find a straightforward solution, either analytic or algorithmic, to this question. You have three types of intersections: intersections between the upper vertices, intersections between the upper and lower vertices, and intersections between the lower vertices. There should be some way to figure out, based on the connectivity of the original regions, the order in which the intersections are laid out.
Here's where things begin to get interesting. Now let's say you wanted to slice this 3D region with some plane and draw the cross section. Since the plane may slice between vertices, you have to look for intersections of the links joining the vertices, both the links within the upper and lower regions and the links between them, with the plane. This still is a relatively easy thing to do. So when you finish this, you've now got a set of M intersection points lying within the plane. Now you want to connect these points and draw your cross section. But in what order do you connect them? At first glance it seems relatively simple, but i can't seem to find a straightforward solution, either analytic or algorithmic, to this question. You have three types of intersections: intersections between the upper vertices, intersections between the upper and lower vertices, and intersections between the lower vertices. There should be some way to figure out, based on the connectivity of the original regions, the order in which the intersections are laid out.